Levitodynamics
Levitodynamics is a branch of optomechanics that represents the study, control and manipulation of nano and microparticles levitated through optical or radiofrequency forces. The field of levitodynamics has seen a fast and steady growth in the past decade, enabled by its potential to study transitions from classical to quantum mechanics, to investigate nonequilibrium statistical physics and to sense extremely small forces and torques [1-10].
In our group we focus our efforts on trapping silica nanoparticles (diameter typically in the order of 100 nm) through optical forces. Recently, we started exploring hybrid traps as well, that make use of both an optical trap and a Paul trap. Our aim is to bring levitodynamics into the quantum regime. To this end, we aim to demonstrate the quantum dynamics of trapped silica nanoparticles (which are macroscopic objects) or entangled motions. This highly ambitious task requires very good nanoparticle isolation and decoherence-free conditions.
Our research pursues different directions:
- Cooling of center of mass motion through either active feedback or passive cavity cooling.
- Study and manipulation of the rotational degrees of freedom of the nanoparticle.
- Development of hybrid trappikng scheme introducing Paul traps.
Optical trapping

Silica nanoparticles are dielectric materials. An external electric field can thus induce a dipole on the nanoparticle and consequently generate a force proportional the field gradient. Optical trapping of silica nanoparticles consists of a strongly focused laser beam, whose strong field gradient generates an optical force strong enough to stably trap the particle in its focus.
The figure above displays one of our optical traps. A strong infrared laser beam propagating towards the right of the image is focused with a high numerical aperture lens. A weaker, green laser beam is overlapped with the trapping beam to make the particle visible by eye. The optical trap is enclosed in a vacuum chamber, within which the air pressure can be freely tuned.
The motion of the particle in the optical trap can be described to first order approximation by a damped harmonic oscillator:
$$m\ddot{x} + m\Gamma_0\dot{x} + m\Omega_0^2 x = \mathcal{F}_\mathrm{th}$$
In the equation, x is one of the three spatial degrees of freedom of the particle, m is the mass, Ω0 is the resonance frequency induced by the optical trap, Fth is a stochastic term representing thermal fluctuations and Γ0 is the damping coefficient. The strength of the thermal fluctuations is connected to the damping force through the fluctuation-dissipation theorem, so that the equipartition theorem holds. An analogous equation holds for the other two degrees of freedom.
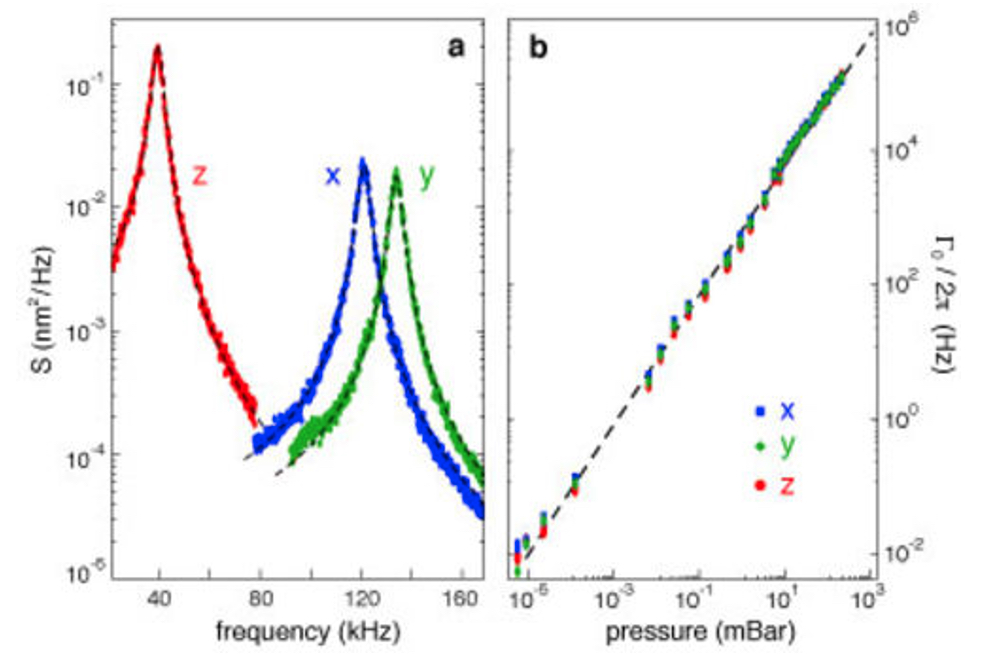
Here we show typical power densities of the three translational modes together with the dependency of the damping coefficient on the vacuum chamber's pressure.
Platform of great isolation, sensing
Such a levitated system represents a platform of great isolation. Indeed the nanoparticle is decoupled from the oscillations of a substrate, the vacuum condition (reaching ultra high vacuum) also isolates it from gas collisions and the very low temperatures reached by using cryostats limit blackbody radiations.
This extreme isolation makes nanoparticles extremely sensitive to small drives such that even thermal fluctuations are easily detected. Their high sensitivity can be exploited to build sensors that can access extremely small forces and torques, such as vacuum friction and Casimir forces. Small statics force can be detected through a free fall protocol, recently demonstrated in our group [7]. The free fall protocol consists of (i) trapping a nanoparticle, (ii) cooling its center of mass motion (see section "Cooling the center of mass"), (iii) turning off the optical trap and letting the particle’s state evolve under the effect of the static force, (iv) turning the optical trap back on and estimating the final state of the particle.
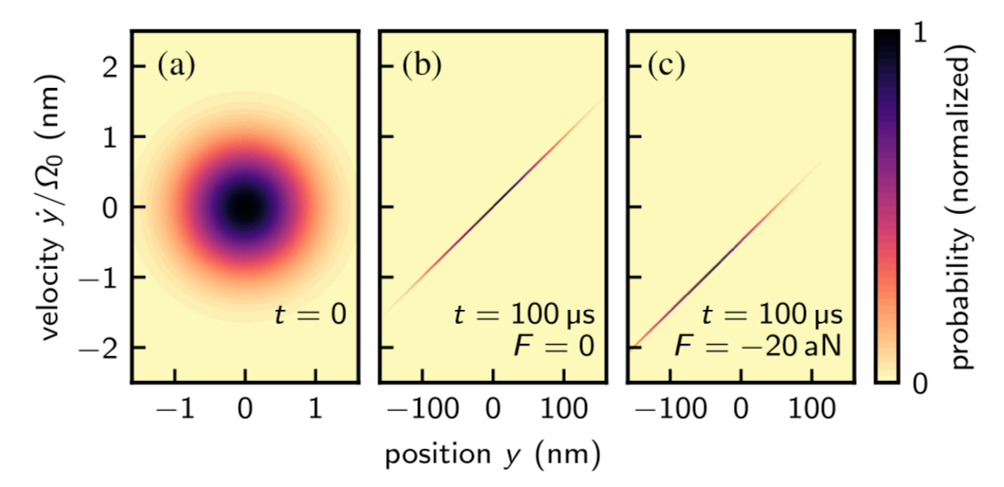
The plot on the left is the theoretical probability distribution of the nanoparticle before the fall (a), after the free fall when only gravity is present (b) and after the fall when both gravity and a 20 aN force drive the particle. Free falls can be applied to particles trapped at subwavelength distances from dielectric surfaces to detect Casimir forces.
However, working with such sensitive systems and at such low pressures is accompanied by experimental challenges. Reaching low pressures from the ambient takes time and direct methods of loading particles into the trap are needed i.e., hollow-core fibers [19] and LIAD [18] (Laser-Induced Accustic Desorption).
Multiple traps
The trapping is not limited to a single laser beam. The combination of several traps is very interesting for various reasons. First, it enables the creation of custom potentials. Recently, we have created a double well trapping potential by using two separate trapping beams. We have used this setup to study the transition rate of the particle, i.e., the average rate at which the particle transitions from one well to the other. By tuning the pressure over a broad range we have observed for the first time the Kramers turnover of the transition rate, a phenomenon that had been elusive for many decades [6].
Having the control over multiple traps also allows us to go even further than the free falls experiments mentioned previously. It enables us to free the particle from one trap and recapture it with a second one drastically increasing the free fall distance.
Furthermore, multiplying the optical traps (i.e., the number of focused laser beams) allows to simultaneously trap several particles and study their interaction.
Cooling the center of mass
The importance of trapping and cooling techniques is evidenced by the series of Nobel Prizes awarded to this theme (1989 ion trapping, 1997 atomic trapping, 2001 Bose-Einstein condensation, 2012 trapping of photons and ions, optical tweezers in 2018). Trapping and cooling of mesoscopic objects, such as the nanoparticles we use, is a new territory that lies at the boundary of classical and quantum physics. To that aim we employ two main approaches: (i) an active feedback force based on the measurement of the particle’s position in free space and (ii) the passive cooling induced by a cavity.
Free space optomechanics
When trapped by an optical beam, the nanoparticle scatters coherent radiation whose phase encodes its position [11]. By extracting the phase through an interferometric measurement, we can reconstruct the position of the nanoparticle and apply a real time feedback force to control its motion.
We make use of two feedback schemes in our experiments:
- Parametric feedback [1, 4]. This method relies on modulating the trapping beam intensity at a frequency equal to twice the particle’s eigenfrequency. When the phase of the modulation is suitably locked to the phase of the particle’s motion, the feedback effectively increases the particle’s damping. The advantage of this scheme is that the same laser beam used to trap the nanoparticle can be additionally used to cool its motion in all three dimensions.
- Cold damping, also called linear feedback [12]. This method applies a force on the particle proportional to its velocity, i.e. a damping force. Cold damping is much easier to model mathematically than parametric feedback, it requires however additional experimental overhead. In general, cold damping allows to reach much lower phonon occupation numbers.
Typically, we employ cold damping on the longitudinal axis (along the beam propagation) and parametric feedback for the other two axes. At low feedback strengths, the phonon occupation is determined by the thermal fluctuations induced by the surrounding air molecules. When the linear feedback is increased, the additional damping contributes to lowering the average phonon occupation number. For very high feedback strengths, measurement back-action is expected: the measurement noise is fed back to the particle, increasing the phonon occupation as a function of the feedback strength [2, 12]. Recently, we have used cold damping to reduce the phonon occupation number below one phonon thus reaching the ground state of motion [20, 21].
Cavity optomechanics
A different paradigm for the cooling of the center of mass motion of the nanoparticle is to combine the optical trap with an optical cavity [3, 13], as shown below (actual setup in lab).

The light scattered by the particle is captured by the cavity and populates the mode closest to the trapping beam’s frequency. Such experimental scheme is called coherent scattering. As the particle moves away from its equilibrium position, the resonance condition of the cavity changes. In turn, the field of the cavity’s mode exerts an optical force on the nanoparticle through dipole interaction. The resulting coupling between the mechanical mode of the particle and the optical mode of the cavity is a rich source of interesting phenomena, including sideband cooling and parametric heating among others.
In our experiments, we blue detune the cavity’s resonance from the trapping beam by an amount equal to the mechanical resonance frequency. Under this condition, the cavity enhances the anti-Stokes photon scattering (which extract mechanical energy from the particle) and hampers the Stokes photon scattering (which in turn increase the particle’s energy). A typical position measurement of the particle is shown below, where the cavity-induced asymmetry in the two sidebands visible.
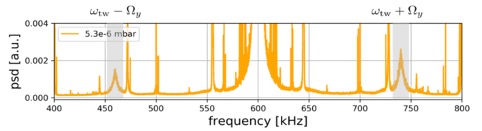
When carefully selecting the position of the particle within the cavity, we have shown that all three dimensions of the particle’s motion can be cooled at the same time [3]. After the achievement of cooling down to the motional ground state one mode of oscillation of the particle [22], we demonstrated the simultaneous motional ground state cooling of two modes [23].
Moreover, adding two traps into the same cavity allows us to study the interaction between the two particles [24], eventually leading to the exploration of many-body effects or the generation of entanglement of motion.
Rotational optomechanics
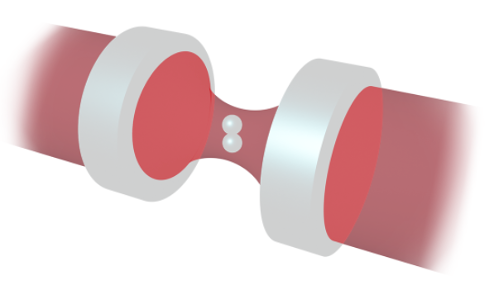
The degrees of freedom of a nanoparticle are not limited to the translational motion. The study of the nanoparticle’s orientation represents a particularly interesting research direction. In order to address the rotational degrees of freedom, we trap nanodumbbells rather than nanoparticles. A trapped nano dumbbell is sketched on the left [14]. The key property of nanodumbbells is their anisotropic polarisability. This enables us not only to detect the dumbbell’s orientation, but also to control it. The behaviour of trapped nanodumbbells changes drastically when trapped with circularly or with linearly polarised light.
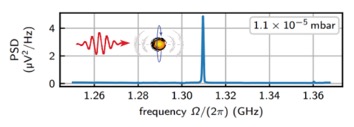
When trapped in a circularly polarised laser beam, the dumbbell starts to rotate very rapidly (see plot on the left) [15]. For pressures below 10^-5 mbar the rotation frequency reaches the GHz regime. This makes optically rotating dumbbells the fasted rotating man-made objects in the world. Due to the high rotation speeds, the particle’s material undergoes enormous strain, which makes rotating particles an interesting platform for investigating material properties.
When trapped in a linearly polarised laser beam, the dumbbell experiences an alignment torque which tends to align the dumbbell to the polarisation direction. The resulting libration around the equilibrium orientation shares many similarities with the translational dynamics of trapped nanoparticles. However, the provided rotational symmetry provides interesting quantum protocols which cannot be performed using translational degrees of freedom. Therefore we aim to bring the libration mode into the quantum regime via feedback cooling.
Hybrid optical-Paul traps
Principle
A Paul trap makes use of a strong oscillating voltage that generates a three-dimensional trap through the ponderomotive force induced on a nanoparticle carrying a net charge. The figure on the left shows the Paul trap chip, inspired from [25], currently in use in the lab.

A major advantage of these chips in comparison to the regular linear Paul traps is their high numerical aperture. Thus it is possible to combine them with optical traps without affecting the trapping capabilities of the latter, allowing for the development of hybrid traps [26]. Paul traps tend to be deeper than optical traps making them ideal "safety nets" to prevent particles from escaping optical traps. Moreover, as the chip geometry is controlled, it opens the way to the generation of customized potentials with the possible introduction of non-harmonic terms.
Trapping of a large variety of particles
The possibility of trapping particles electrically rather than optically opens the possibility of trapping absorbing particles. So far limited to trapping silica particles under vacuum conditions, the trapping of gold particles is very promising for spectroscopy purposes. Indeed with levitated spectroscopy, the influence of the substrates disappears. Furthermore, broadening the spectrum of the particles that we can trap opens the path to trap particles carrying a spin degree of freedom, e.g., nanodiamonds with NV centers [28].
Towards quantum experiments
As mentioned above, when a nanoparticle is trapped by an optical beam, it absorbs light. Moreover the light it scatters encodes information about the position of the nanoparticle. Whether an experimentalist records the phase of the particle or not, the position of the nanoparticle is being continuously measured by the trapping beam. Such a continuous measurement is a source of quantum decoherence, since the environment is continuously monitoring the particle’s state, thus contaminating its purity.
Despite their deleterious effect on the state’s purity, optical traps are essential for state preparation, as they allow efficient measure and control of its degrees of freedom. Since the charge of the nanoparticle can in general be controlled, a particularly promising solution to the decoherence problem is to combine the optical trap with a Paul trap. Among several, three main applications of hybrid traps we aim at are:
- Measuring decoherence and reheating rates of a nanoparticle evolving in a Paul trap in the absence of photons.
- Squeezing mechanical state of a nanoparticle to expand its wave function. We already demonstrated thermal squeezing of a ratio of 25 by applying a so-called "frequency jump protocol" where, after an initialisation (cooling of its center of mass) in the optical trap the particle is led to evolve in the Paul trap for a fixed duration [27].
- Introduce nonlinearities in the potential to be able to measure negativity of the Wigner function.
Related publications
[1] J. Gieseler, B. Deutsch, R. Quidant, and L. Novotny, ”Sub-Kelvin parametric feedback cooling of a laser-trapped nanoparticle,” Phys. Rev. Lett. 109, 103603 (2012).
[2] F. Tebbenjohanns et al., "Motional Sideband Asymmetry of a Nanoparticle Optically Levitated in Free Space", Phys. Rev. Lett. 124, 013603 (2020).
[3] D. Windey et al., "Cavity-Based 3D Cooling of a Levitated Nanoparticle via Coherent Scattering", Phys. Rev. Lett. 122, 123601 (2019).
[4] V. Jain et al., "Direct Measurement of Photon Recoil from a Levitated Nanoparticle", Phys. Rev. Lett. 116, 243601 (2016).
[5] J. Gieseler et al., "Nonlinear mode coupling and synchronisation of vacuum-trapped nanoparticles", Phys. Rev. Lett. 112, 103603 (2014).
[6] L. Rondin et al., "Direct measurement of the Kramers turnover", Nat. Nanotech. 12, 1130 (2017).
[7] E. Hebestreit et al., "Sensing Static Forces with Free-Falling Nanoparticles", Phys. Rev. Lett. 121, 063602 (2016).
[8] G. Ranjit et al., "Zeptonewton force sensing with nano spheres in an optical lattice", Phys. Rev. A (2016).
[9] F. van der Laan et al., "Optically levitated rotor at its thermal limit of frequency stability", Phys. Rev. A. 102, 013505 (2020).
[10] R. Diehl, "Optical levitation and feedback cooling of a nanoparticle at sub wavelength distances from a membrane", Phys.Rev.A, 98, (2018).
[11] S. Lindner et al., "Hollow-core fiber loading into ultra-high vacuum", arXiv preprint arXiv:2311.13920 (2023).
[12] D.S. Bykov et al., "Direct loading of nanoparticles under high vacuum into a Paul trap for levitodynamical experiments", Appl. Phys. Lett. 115.3 (2019).
[13] F. Tebbenjohanns et al., "Optimal position detection of a dipolar scatterer in a focused field", Phys. Rev. A. 100, 043821 (2019).
[14] F. Tebbenjohanns et al., "Cold Damping of an Optically Levitated Nanoparticle to Microkelvin Temperatures", Phys. Rev. Lett. 122, 223601 (2019).
[15] F. Tebbenjohanns et al., "Quantum control of a nanoparticle optically levitated in cryogenic free space", Nature 595.7867 (2021): 378-382.
[16] L. Magrini et al., "Real-time optimal quantum control of mechanical motion at room temperature", Nature 595.7867 (2021): 373-377.
[17] M. Aspelmeyer, T. J. Kippenberg, F. Marquardt, "Cavity Optomechanics", Springer (2014).
[18] U. Delić et al., "Cooling of a levitated nanoparticle to the motional ground state", Science 367.6480 (2020): 892-895.
[19] J. Piotrowski et al., "Simultaneous ground-state cooling of two mechanical modes of a levitated nanoparticle", Nat. Phys. (2023): 1-5.
[20] J. Vijayan et al., "Cavity-mediated long-range interactions in levitated optomechanics", arXiv preprint arXiv:2308.14721 (2023).
[21] The illustration has been provided by S. Papadopoulos.
[22] R. Reimann et al., "GHz Rotation of an Optically Trapped Nanoparticle in Vacuum", Phys. Rev. Lett. 121, 033602 (2018).
[23] J.-S Chen, "Ticking near the zero-point energy: towards accuracy in optical clocks", Ph.D. thesis, Univ. of Colorado (2017).
[24] E. Bonvin et al., "Hybrid Paul-optical trap with large optical access for levitated optomechanics", arXiv preprint arXiv:2312.10131 (2023).
[25] G. P. Conangla et al., "Motion control and optical interrogation of a levitating single nitrogen vacancy in vacuum", Nano Lett. 18.6 (2018): 3956-3961.
[26] E. Bonvin et al., "State expansion of a levitated nanoparticle in a dark harmonic potential", arXiv preprint arXiv:2312.13111 (2023).


